La realtà quantistica: un viaggio tra i mattoncini elementari dell’universo

Quest’opera contiene in larga parte contenuti generati dall’intelligenza artificiale. L’intervento umano è stato centrale nell’organizzazione degli argomenti, nella revisione e nella cura del prodotto finale. Edizione 1.3 © 2025

Introduzione

Da oltre un secolo, la fisica quantistica continua a sorprendere chiunque vi si avvicini. Le sue leggi sembrano intrecciarsi in modi che sfuggono alla consuetudine, disegnando una realtà che va ben oltre il senso comune e la percezione diretta. Fenomeni come particelle che sembrano trovarsi in più luoghi contemporaneamente, entità che si comportano sia come onde che come particelle, e connessioni istantanee tra oggetti distanti, contribuiscono a questa percezione. Molti considerano tali idee come paradossi inspiegabili, relegandoli a un ambito arcano accessibile solo a pochi eletti. Ma è davvero così strana la fisica quantistica? O è piuttosto la nostra prospettiva, modellata dalla realtà macroscopica, che la rende tale?

Nel film I ragazzi di Via Panisperna (1988), diretto da Gianni Amelio, viene raccontato uno snodo cruciale di questa storia: la scoperta sperimentale di fenomeni che sfuggivano a ogni previsione. A metà degli anni Trenta, la struttura teorica della meccanica quantistica era già solida e riconosciuta dalla comunità scientifica. Ma applicarla ai nuclei atomici, a particelle appena scoperte come il neutrone, significava inoltrarsi in un terreno quasi inesplorato. La fisica nucleare era ancora giovane, e le risposte che emergevano dal laboratorio spesso apparivano incoerenti, elusive, talvolta beffarde.

Una scena del film cristallizza con forza questo senso di disorientamento. Un giovane collaboratore di Enrico Fermi, sopraffatto da risultati sperimentali che non trovavano spiegazione nei modelli disponibili, pronuncia parole che oscillano tra la frustrazione e la poesia:

“Sai che differenza c’è tra una cosa morta e una viva? Che la cosa morta si comporta sempre allo stesso modo, qualunque stimolo tu le dai. Quella viva no. Bella scoperta, eh! Ci sono arrivato questa notte: secondo me l’uranio è come un essere umano, ha un’anima, si sta divertendo alle nostre spalle. Altrimenti non mi spiego questi dati. Che sta succedendo, professore?”

Questa battuta non è solo il segno di un fallimento momentaneo: è il sintomo di un passaggio epocale. La materia radioattiva sembrava rispondere in modo incoerente ai tentativi di manipolazione, e questo scarto tra aspettativa e realtà apriva interrogativi che andavano oltre le formule, toccando il senso stesso dell’indagine scientifica.

Oggi, fenomeni come la fissione, l’interazione tra neutroni e nuclei pesanti, o la natura probabilistica degli eventi a livello subatomico, ci appaiono parte di un linguaggio consolidato. Ma all’epoca erano vertigini. Il dialogo di quella scena coglie un momento in cui la fisica sembrava vacillare, non perché mancassero teorie, ma perché si stava tentando di applicarle a un mondo ancora troppo poco conosciuto. In fondo, ciò che rende la meccanica quantistica tanto destabilizzante non è la sua logica interna, ma il modo in cui continua a spingere i confini della nostra immaginazione.

Nel nostro quotidiano, ci muoviamo in un mondo governato da leggi fisiche intuitive: gli oggetti hanno posizioni e velocità definite, le cause precedono gli effetti in modo lineare, e possiamo misurare le proprietà delle cose senza alterarle. Queste aspettative derivano da millenni di evoluzione e interazione con un ambiente che opera su scale ben diverse da quelle atomiche e subatomiche. Tuttavia, quando ci addentriamo nel regno dell’infinitamente piccolo, scopriamo che queste leggi intuitive non si applicano più così facilmente. Le particelle subatomiche seguono regole che possono sembrare controintuitive o addirittura paradossali, se viste attraverso le lenti delle nostre categorie percettive abituali.

È essenziale comprendere che la fisica quantistica non è illogica o assurda; piuttosto, richiede un cambiamento nel nostro modo di pensare. Come esploratori che si avventurano in terre sconosciute, dobbiamo essere disposti a mettere in discussione le nostre assunzioni e ad abbracciare nuovi paradigmi. Solo così potremo cogliere la logica sottostante ai fenomeni quantistici e apprezzare la coerenza interna di questa teoria che, nonostante la sua complessità, descrive con precisione il comportamento fondamentale della natura.

Questo saggio ha come obiettivo guidare il lettore in un viaggio alla scoperta dei principi della fisica quantistica, rendendoli accessibili attraverso un linguaggio chiaro, evitando spiegazioni tecniche e dettagli storici troppo complessi. Ci concentreremo su esperimenti mentali, analogie e considerazioni filosofiche per illuminare concetti che altrimenti potrebbero sembrare astratti. Vogliamo dimostrare che, con il giusto approccio, è possibile comprendere questi fenomeni senza cedere all’idea che siano paradossi inspiegabili o accettare passivamente idee che sembrano sfidare la logica.

Attraverso esperimenti mentali audaci, esploreremo come le nostre intuizioni, apparentemente solide nel mondo macroscopico, possano rivelarsi ingannevoli se applicate alla realtà quantistica. Questi strumenti ci permetteranno di affrontare concetti come il principio di sovrapposizione, il dualismo onda-particella, la quantizzazione dell’energia, il collasso della funzione d’onda e l’entanglement in modo coinvolgente e intuitivo.

Invitiamo quindi il lettore ad avvicinarsi a questo saggio con mente aperta e curiosità, pronto a esplorare nuovi orizzonti e a sfidare le proprie percezioni. Speriamo che, attraverso questo percorso, si possa apprezzare la bellezza e la coerenza della fisica quantistica, riconoscendo che, oltre le apparenze controintuitive, esiste una logica profonda che governa il mondo subatomico. Solo accettando che le nostre categorie percettive devono evolversi, possiamo davvero comprendere e abbracciare la realtà quantistica.

Capitolo 1: Rompere le barriere della percezione macroscopica

1.1 La percezione comune della fisica quantistica come strana o illogica

La fisica quantistica ha spesso suscitato un senso di spaesamento, alimentando l’idea che sia una scienza al di fuori della comprensione comune, quasi un territorio in cui la realtà si piega a regole inconcepibili. La sua fama di disciplina “strana” o “paradossale” non nasce solo dalla sua complessità intrinseca, ma anche dalle interpretazioni che nel tempo ne hanno amplificato il fascino misterioso. Da un lato, la cultura pop e la fantascienza hanno mitizzato i fenomeni quantistici, trasformandoli in concetti ai confini della magia; dall’altro, correnti di pensiero più speculative hanno enfatizzato aspetti apparentemente mistici, come la sovrapposizione degli stati o l’influenza dell’osservatore sul sistema osservato. Tuttavia, al di là delle narrazioni sensazionalistiche, la meccanica quantistica rimane un modello solido e rigoroso, capace di descrivere il comportamento della materia con un’accuratezza senza precedenti.

L’idea che una particella possa trovarsi in più luoghi contemporaneamente o che l’osservazione possa alterare il risultato di un esperimento, se presentata senza il contesto adeguato, alimenta la percezione della fisica quantistica come una sorta di magia scientifica, lontana dalla realtà quotidiana e inaccessibile alla comprensione comune. I media tendono a esagerare questi aspetti enigmatici, contribuendo a creare un’immagine distorta della disciplina e scoraggiando molti dall’approfondirne la conoscenza, convinti della sua complessità.

Anche l’uso di una terminologia tecnica e di formalismi matematici avanzati rafforza questa percezione di inaccessibilità. La mancanza di una divulgazione chiara, che renda i concetti fondamentali più comprensibili senza banalizzarli, ha consolidato l’idea che la fisica quantistica sia riservata a pochi esperti.

Pur sfidando molte delle nostre intuizioni quotidiane, la fisica quantistica non è illogica o incomprensibile. Al contrario, è una struttura teorica altamente coerente, basata su principi matematici solidi, che descrive con precisione il comportamento della materia e dell’energia a livello fondamentale. Le sue previsioni sono state confermate da numerosi esperimenti e hanno portato a innovazioni tecnologiche che usiamo quotidianamente.

Questa percezione di enigmaticità affonda le radici nel nostro istinto di trasferire i parametri del mondo visibile a dimensioni in cui questi strumenti di lettura risultano inadeguati. Quando queste aspettative non vengono soddisfatte, è facile considerare i fenomeni quantistici strani o illogici.

Per superare questa percezione comune, è necessario rendere la fisica quantistica più accessibile e comprensibile, senza semplificazioni eccessive. Attraverso analogie efficaci, esperimenti mentali e una presentazione chiara dei concetti chiave, è possibile mostrare come questi fenomeni siano non solo comprensibili, ma anche profondamente coerenti con la struttura dell’universo.

1.2 L’importanza di adattare le nostre categorie mentali al mondo subatomico

Il modo in cui interpretiamo la realtà è il risultato di un lungo processo di adattamento, basato sulle leggi fisiche che sperimentiamo ogni giorno. Nella nostra esperienza, il mondo appare stabile e prevedibile, con schemi profondamente radicati nella percezione e consolidati dalla cultura e dalla scienza classica. Questi modelli plasmano il nostro modo di pensare e rendono difficile accettare una visione dell’universo in cui la materia si comporta in modo imprevedibile, al di fuori delle regole familiari che regolano la realtà quotidiana.

Quando ci addentriamo nel regno microscopico, questi schemi iniziano a mostrare i loro limiti. Le particelle subatomiche non seguono le stesse regole degli oggetti macroscopici, comportandosi in modi che sfidano le nostre intuizioni più profonde. Una particella, ad esempio, può esistere in una sovrapposizione di stati, occupando simultaneamente più posizioni o assumendo diverse proprietà fino al momento della misurazione, concetto che contrasta con la nostra esperienza quotidiana di oggetti che occupano un singolo luogo in un determinato momento.

Comprendere il mondo subatomico significa riprogrammare la bussola interiore con cui interpretiamo la realtà. Se insistiamo nell’applicare le regole e le intuizioni del mondo macroscopico, rischiamo di fraintendere o considerare illogici i comportamenti delle particelle. Questo adattamento richiede uno sforzo intellettuale: dobbiamo mettere in discussione le nostre assunzioni di base e accettare che la natura possa operare secondo principi diversi da quelli a cui siamo abituati.

Un utile paragone è l’apprendimento di una nuova lingua o cultura. Quando ci immergiamo in un ambiente diverso, scopriamo che le nostre abitudini e aspettative potrebbero non applicarsi. Comprendere una nuova lingua non significa soltanto memorizzare parole e regole grammaticali, ma anche abituarsi a una diversa logica del pensiero e della comunicazione. Allo stesso modo, per comprendere il mondo quantistico, dobbiamo adottare nuovi paradigmi concettuali.

Ad esempio, il concetto di determinismo, centrale nella fisica classica, deve essere rivisto. Nella meccanica quantistica, il comportamento di una particella è descritto in termini di probabilità, non di certezza. Questo non significa che la natura sia priva di regole, ma che queste operano su una base statistica anziché deterministica. Accettare questo cambiamento di prospettiva è fondamentale per comprendere fenomeni come il decadimento radioattivo o l’effetto tunnel.

Inoltre, il ruolo dell’osservatore diventa cruciale. Nella fisica classica, l’osservatore è esterno al sistema e non lo influenza. Nel mondo quantistico, invece, l’atto di misurare altera lo stato della particella, portando al “collasso della funzione d’onda”. Questo fenomeno ci costringe a riconsiderare la separazione tra osservatore e oggetto osservato, aprendo nuove riflessioni sulla natura della realtà.

Adattare le nostre categorie mentali non significa abbandonare la logica o il rigore scientifico. Al contrario, significa arricchire i nostri strumenti concettuali per includere nuove possibilità. Significa riconoscere che le nostre intuizioni, per quanto utili nel contesto quotidiano, non sono universali e possono essere inadeguate per descrivere fenomeni fuori dalla nostra esperienza diretta.

Questo tipo di adattamento è avvenuto anche in altri momenti chiave della scienza. L’introduzione della teoria della relatività di Einstein, ad esempio, ha richiesto un cambiamento radicale nel modo in cui concepiamo tempo e spazio. Allo stesso modo, la fisica quantistica ci invita a ripensare concetti come causalità, identità e località.

Abbracciando nuovi paradigmi, possiamo superare le limitazioni imposte dalle nostre intuizioni e scoprire una realtà ancora più affascinante e complessa. Questo sforzo è al cuore del progresso scientifico ed è una sfida entusiasmante per chiunque voglia esplorare il mondo quantistico.

1.3 Obiettivi del saggio e metodologia basata su esperimenti mentali

L’obiettivo principale di questo saggio è demistificare la fisica quantistica, presentandola non come un insieme di paradossi insolubili o fenomeni inspiegabili, ma come una teoria scientifica coerente che descrive accuratamente il comportamento della natura a livello subatomico. Per raggiungere questo scopo, utilizzeremo una metodologia basata su esperimenti mentali, analogie e considerazioni filosofiche. Gli esperimenti mentali agiranno come bussole immaginarie, capaci di orientarci in un territorio altrimenti inaccessibile. Ci aiuteranno a costruire ponti tra intuizione e teoria, trasformando scenari astratti in orizzonti comprensibili. Usati anche da Einstein (Gedankenexperimente) questi esperimenti mettono in luce le implicazioni dei principi quantistici in modo intuitivo, collegando idee astratte a esperienze più familiari e rendendo accessibili concetti teorici spesso difficili da visualizzare in modo concreto.

Nel corso del saggio, introdurremo esperimenti mentali originali per affrontare concetti chiave come il principio di sovrapposizione, il dualismo onda-particella, la quantizzazione dell’energia, il collasso della funzione d’onda e l’entanglement. Questi esperimenti chiariranno tali concetti, dimostrando come essi siano logici e coerenti all’interno della fisica quantistica.

Inoltre, integreremo elementi di matematica, utilizzando il formalismo di Dirac, noto anche come notazione bra-ket, per fornire una base più rigorosa alla nostra discussione. Questo formalismo permetterà di descrivere in modo conciso e preciso gli stati fisici e le osservabili, senza sovraccaricare il discorso di dettagli tecnici superflui. Tuttavia, il formalismo matematico non è necessario né fondamentale per seguire il ragionamento di questo saggio, e potrà essere anche ignorato senza perdere la comprensione dei concetti essenziali. L’intento è offrire una comprensione più profonda dei concetti, mostrando come la matematica sia uno strumento utile, ma non indispensabile, per descrivere i fenomeni quantistici.

Le considerazioni filosofiche avranno un ruolo significativo nel nostro approccio. Esploreremo le implicazioni dei principi quantistici sulla nostra comprensione della realtà, della causalità e del ruolo dell’osservatore. Questo contribuirà a contestualizzare i concetti scientifici in una cornice più ampia, mettendo in luce come la fisica quantistica non solo abbia rivoluzionato la scienza, ma abbia anche influenzato profondamente il nostro modo di concepire la realtà.

Il saggio si propone quindi come una guida nel mondo della fisica quantistica, mantenendo un equilibrio tra semplicità e rigore. Eviteremo spiegazioni eccessivamente tecniche o dettagli storici complessi, concentrandoci su ciò che è essenziale per comprendere i principi fondamentali. Vogliamo coinvolgere il lettore in un dialogo intellettuale stimolante, che lo porti a riconsiderare le proprie intuizioni e ad abbracciare nuovi modi di pensare.

Questo viaggio nella fisica quantistica vuole essere non solo un’esplorazione scientifica, ma anche un invito a espandere la nostra percezione del possibile. Spingendoci oltre le cornici abituali, scopriremo come la coerenza del mondo subatomico, per quanto diversa da ciò che ci è familiare, si riveli straordinariamente armoniosa. Lungi dall’essere un regno di assurdità, la fisica quantistica è una finestra sulla complessità e la bellezza dell’universo a livello fondamentale. Invitiamo il lettore a unirsi a questa esplorazione con mente aperta e curiosità.

Capitolo 2: L’Esperimento dei mattoncini Lego

2.1 Descrizione dell’esperimento

Immaginiamo di trovarci in un vasto spazio aperto, senza confini, con davanti a noi una montagna virtualmente infinita di mattoncini Lego, quei pezzi semplici che molti di noi hanno utilizzato nell’infanzia. Con una tale abbondanza di mattoncini e uno spazio illimitato, le possibilità creative sono infinite. Possiamo dare vita a tutto ciò che la nostra immaginazione concepisce: costruire città con edifici dettagliati, ponti, veicoli e persino creature mitologiche o preistoriche, come un tirannosauro a grandezza naturale.

In questa condizione ideale, ogni dettaglio è realizzabile. Possiamo aggiungere finestre, foglie agli alberi, e persino espressioni facciali ai personaggi. Ogni mattoncino arricchisce il progetto, permettendoci di creare forme sempre più complesse e dettagliate, senza limiti dettati dalla quantità o dallo spazio.

Ora, immaginiamo che la quantità di mattoncini a nostra disposizione inizi a diminuire gradualmente. Forse la montagna di pezzi non è più infinita, o ci siamo imposti un limite per sfidare la nostra creatività. Con una quantità ancora considerevole, possiamo comunque realizzare molte idee, ma dobbiamo iniziare a fare delle scelte: sacrificare dettagli, semplificare parti delle costruzioni o combinare elementi in modo più efficiente.

Con la riduzione continua della scorta di mattoncini, le limitazioni diventano sempre più evidenti. Le nostre creazioni si fanno necessariamente più piccole e meno dettagliate. Dovremo dire addio alla possibilità di realizzare la Morte Nera o il Millenium Falcon. I dettagli più minuti devono essere eliminati, concentrando i pezzi sulle strutture principali.

Quando i mattoncini iniziano a scarseggiare, le nostre possibilità creative si restringono drasticamente. Siamo confinati a costruzioni estremamente semplici, come cubi, torri o muri, mentre le combinazioni possibili diventano sempre più limitate. Il concetto stesso di “forma” inizia a perdere il significato che aveva prima, poiché non siamo più in grado di creare strutture complesse, ma solo di assemblare i pochi pezzi rimasti in modi essenziali e ripetitivi. Inoltre, il semplice aggiungere o rimuovere un singolo mattoncino può cambiare e stravolgere l’intera struttura, mentre con molti mattoncini a disposizione queste variazioni sarebbero state irrilevanti, passando inosservate.

Infine, con un numero esiguo di mattoncini, la nostra capacità creativa è quasi azzerata. Non possiamo più creare nulla di significativo o riconoscibile, e il gioco creativo si trasforma in un’osservazione dei singoli pezzi senza la possibilità di combinarli in modo rilevante.

Questo esperimento mentale ci porta a riflettere su come la quantità di elementi fondamentali influenzi la nostra capacità di creare e percepire forme complesse. Con risorse significative, il mondo delle possibilità è vasto. Man mano che le risorse diminuiscono, le opzioni si restringono, e le nostre categorie percettive, abituate alla complessità, devono adattarsi a una realtà più semplice e limitata. Alla fine, quando le risorse sono ridotte al minimo, le nozioni di forma e complessità diventano inapplicabili nel modo in cui le conosciamo.

Questo scenario con i mattoncini Lego mostra chiaramente come la quantità e la scala degli elementi disponibili influenzino ciò che possiamo costruire e percepire. Ci spinge a riflettere su come, a un livello più profondo, le nostre intuizioni e aspettative, formate nel mondo macroscopico, possano diventare inadeguate, preparando così il terreno per un’analogia con il comportamento delle particelle elementari e la fisica quantistica.

2.2 Analogia con le particelle elementari

L’esperimento mentale dei mattoncini Lego è una metafora per comprendere le differenze tra il mondo subatomico e la realtà che percepiamo quotidianamente. I mattoncini rappresentano le particelle elementari, i costituenti fondamentali della materia. Così come i mattoncini permettono di costruire strutture semplici o complesse, le particelle elementari formano atomi, molecole e, in definitiva, tutto ciò che esiste nell’universo.

Quando disponiamo di un numero enorme di mattoncini, le possibilità creative sono infinite, e possiamo realizzare strutture elaborate. Allo stesso modo, nel mondo macroscopico, l’interazione di un’enorme moltitudine di atomi genera gli oggetti e i fenomeni che osserviamo quotidianamente. Proprietà come la solidità o la fluidità emergono dall’interazione collettiva di una quantità sterminata di particelle a livello microscopico.

Man mano che ci adattiamo a dimensioni più piccole, limitando il numero di mattoncini impiegabili, le possibilità di costruzione diminuiscono. Con pochi pezzi, non possiamo più creare forme complesse; siamo limitati a strutture semplici. Questa situazione riflette ciò che accade nel mondo atomico e subatomico. Le nostre categorie percettive, sviluppate per interpretare la realtà macroscopica, non sono più applicabili: ad esempio non possiamo più parlare di “forma” o “struttura” nel senso tradizionale, perché le proprietà delle particelle elementari non si manifestano come quelle degli oggetti che conosciamo.

Abbiamo appena usato le parole sterminato o moltitudine per esprimere come il macroscopico sia costituito da particelle, ma è meglio chiarire la scala con qualche numero. Un granello di sabbia, con un diametro di circa 0,5 millimetri, è composto da un numero enorme di atomi, generalmente nell’ordine di 10¹⁹ (ovvero dieci miliardi di miliardi). Anche un oggetto apparentemente piccolo come una cellula umana, che misura in media 10 micrometri (10⁻⁵ metri), contiene circa 100 trilioni di atomi.

Questi numeri mostrano come la realtà che percepiamo sia composta da un numero incredibilmente alto di particelle elementari, ognuna delle quali segue le leggi della meccanica quantistica. Tuttavia, quando milioni di miliardi di particelle interagiscono tra loro, gli effetti quantistici tendono a sfumare, dando origine a comportamenti collettivi che risultano familiari e prevedibili su scala macroscopica.

Nel mondo subatomico, le particelle elementari non sono versioni in miniatura degli oggetti macroscopici. Non possiedono una posizione o una velocità definite come le intendiamo comunemente. Secondo il principio di indeterminazione di Heisenberg, esiste un limite alla precisione con cui possiamo conoscere simultaneamente la posizione e la quantità di moto di una particella, il che rende i concetti di “posizione esatta” e “traiettoria determinata” inapplicabili a queste scale.

Un altro aspetto fondamentale è il dualismo onda-particella. Le particelle elementari, come elettroni e fotoni, possono comportarsi sia come particelle sia come onde. Questa dualità non ha un corrispettivo nel mondo macroscopico e sfida profondamente le nostre categorie concettuali. Nell’analogia dei mattoncini, è come se i pezzi potessero comportarsi talvolta come oggetti discreti, come quelli che abbiamo imparato a conoscere grazie ai nostri sensi, talvolta come una struttura continua e sfuggente, a seconda delle circostanze.

La quantizzazione dell’energia trova un ulteriore parallelo nell’esperimento mentale. Così come con un numero limitato di mattoncini possiamo costruire solo determinate forme, nel mondo quantistico le particelle possono assumere solo valori discreti di energia. Le transizioni energetiche non sono continue, ma avvengono in “salti” quantizzati, proprio come i mattoncini possono essere aggiunti o rimossi solo in unità intere.

Nell’universo dei mattoncini limitati, le nozioni di ‘grande’ e ‘piccolo’, ‘complesso’ e ‘semplice’ si trasformano, perdendo il loro significato abituale. Analogamente, nel mondo delle particelle elementari, i concetti con cui interpretiamo la realtà macroscopica diventano inadeguati. Qui, la struttura sfuma nell’indeterminazione, la continuità si spezza in quantità discrete, e le traiettorie cedono il passo a probabilità. Non è un mondo privo di logica, ma uno in cui le regole che crediamo universali si rivelano relative al nostro livello di osservazione. Comprenderlo significa accettare che la realtà non è unica e immutabile, ma varia a seconda della scala a cui la osserviamo.

2.3 Come le nostre categorie percettive si infrangono a scale subatomiche

Nel mondo macroscopico, pensiamo a un oggetto come avente una posizione specifica in un dato momento. Una sedia è in una stanza, un albero è in un parco. Nel mondo quantistico, invece, le particelle possono trovarsi in una sovrapposizione di stati, occupando più posizioni contemporaneamente fino al momento della misurazione. Questo fenomeno sfida la nostra intuizione e richiede una revisione del concetto di presenza e localizzazione.

Il principio di indeterminazione di Heisenberg mette ulteriormente in crisi queste categorie. Non è possibile conoscere simultaneamente e con precisione la posizione e la quantità di moto di una particella (nella fisica classica la quantità di moto è legata alla velocità). Questa limitazione non è tecnologica, ma intrinseca alla natura quantistica. L’idea di una traiettoria definita, così familiare nel mondo macroscopico, perde significato a livello subatomico, rendendo inoltre indistinguibili le particelle identiche localizzabili in un determinato spazio, poiché non è possibile seguirne la traiettoria con precisione ed etichettarle come entità univoche (cosa che impedirà a una singola parte del sistema quantistico di poter essere misurata senza influenzare le restanti.)

Allora come mai negli esperimenti condotti negli acceleratori di particelle vediamo chiaramente percorsi ben delineati? Le immagini prodotte da questi esperimenti mostrano tracciati curvi e ordinati, che sembrano ricalcare il comportamento delle particelle così come lo descriverebbe la fisica classica. Non è forse una contraddizione con il principio di indeterminazione e con l’impossibilità di assegnare una posizione precisa a una particella quantistica?

La risposta risiede nel fatto che, a energie molto elevate, la fisica classica riemerge come un limite naturale della meccanica quantistica. Quando una particella si muove ad alta velocità e interagisce continuamente con il mezzo circostante, gli effetti quantistici più sottili, come la sovrapposizione di stati e l’indeterminazione marcata della posizione, diventano meno rilevanti. In queste condizioni, la dinamica delle particelle diventa più prevedibile e, sebbene ogni interazione segua ancora le leggi della meccanica quantistica, il loro comportamento complessivo assume caratteristiche più familiari.

Negli acceleratori di particelle, le tracce che osserviamo nei rivelatori non sono la rappresentazione diretta del movimento di una particella nel senso classico, ma il risultato dell’interazione della particella con il mezzo di rilevazione. Quando una particella carica attraversa un rivelatore, interagisce con gli atomi del materiale, ionizzandoli o inducendo emissioni di luce. Questa serie di interazioni lascia una sequenza di segnali puntuali, che possono poi essere analizzati per ricostruire il percorso della particella.

Ciò che vediamo non è quindi la traiettoria della particella nel senso classico di un oggetto che segue un cammino continuo e determinato in ogni istante, ma una ricostruzione basata sulle sue interazioni con l’ambiente circostante. Questo fenomeno spiega perché a certe scale energetiche il comportamento delle particelle possa apparire più simile a quello previsto dalla fisica classica: la meccanica quantistica non viene meno, ma le condizioni sperimentali portano a un comportamento che, a livello macroscopico, può essere interpretato in termini di traiettorie definite.

Facciamo ora un elenco completo degli aspetti più controversi dei sistemi quantistici:

Il dualismo onda-particella sfida un’altra delle nostre categorie percettive. Nel mondo macroscopico, distinguiamo chiaramente tra oggetti materiali e onde. Una pietra lanciata in uno stagno è un oggetto materiale, mentre le increspature che si propagano sono onde. In meccanica quantistica, però, le particelle elementari possono comportarsi sia come particelle che come onde, a seconda dell’esperimento. Questa dualità non ha un equivalente diretto nella nostra esperienza quotidiana.

Anche il concetto di energia continua viene messo in discussione. Nel mondo macroscopico, l’energia di un sistema può variare in modo continuo all’interno di un certo intervallo. Nel mondo quantistico, invece, l’energia può essere sia continua sia quantizzata, a seconda del sistema considerato. In molti sistemi quantistici, l’energia assume solo valori discreti e le transizioni tra questi livelli avvengono attraverso “salti” quantici, anziché in modo fluido e continuo.

Il fenomeno dell’entanglement quantistico infrange il concetto di separazione tra oggetti distanti. Due particelle entangled, anche se separate da grandi distanze, influenzano istantaneamente l’una lo stato dell’altra, sfidando il principio di località, cardine della fisica classica.

Il collasso della funzione d’onda introduce ulteriori complicazioni. Nel mondo macroscopico, l’atto di osservare non altera significativamente l’oggetto osservato. Possiamo misurare la temperatura di un oggetto senza modificarla. Nel mondo quantistico, invece, l’osservazione stessa altera lo stato del sistema: prima della misurazione, una particella può essere in una sovrapposizione di stati; dopo la misurazione, si trova in uno stato definito. L’osservatore diventa parte integrante del sistema osservato.

La frattura tra senso comune e realtà quantistica non deve essere vista come un ostacolo, ma come un’opportunità per espandere la nostra comprensione. Richiede l’adozione di nuovi paradigmi concettuali e l’accettazione di idee che, pur controintuitive, sono supportate da solide evidenze sperimentali. Dobbiamo essere disposti a mettere in discussione le nostre assunzioni e abbracciare un pensiero più flessibile.

Accettare che le nostre categorie percettive si infrangono a scale subatomiche è dunque fondamentale per comprendere la fisica quantistica. Ci permette di avvicinarci a questi fenomeni con una mente aperta, pronti a scoprire una logica che, pur differente dalle nostre intuizioni, è coerente e rigorosa. Questo cambiamento di prospettiva arricchisce la nostra conoscenza scientifica e amplia la nostra visione dell’universo.

Capitolo 3: Principi Fondamentali della Fisica Quantistica

3.1 Il Dualismo Onda-Particella

Uno dei concetti più affascinanti e controintuitivi della fisica quantistica è il dualismo onda-particella, che afferma che tutte le particelle elementari, come elettroni, fotoni e protoni, possiedono sia proprietà ondulatorie che corpuscolari. Ciò che nel mondo macroscopico percepiamo come distinti, onde e particelle, nel mondo quantistico sono aspetti complementari di una stessa realtà.

L’esperimento della doppia fenditura è un esempio emblematico del dualismo onda-particella. Immaginiamo una sorgente che emette elettroni uno alla volta verso una barriera con due fessure. Se gli elettroni si comportassero esclusivamente come particelle, ci aspetteremmo di vedere due bande sullo schermo, corrispondenti alle fessure. Invece, si osserva un pattern di interferenza, tipico delle onde, con bande alternate dovute all’interferenza costruttiva e distruttiva. Anche inviando gli elettroni uno alla volta, il pattern emerge, suggerendo che ogni elettrone interferisca con se stesso come un’onda distribuita.

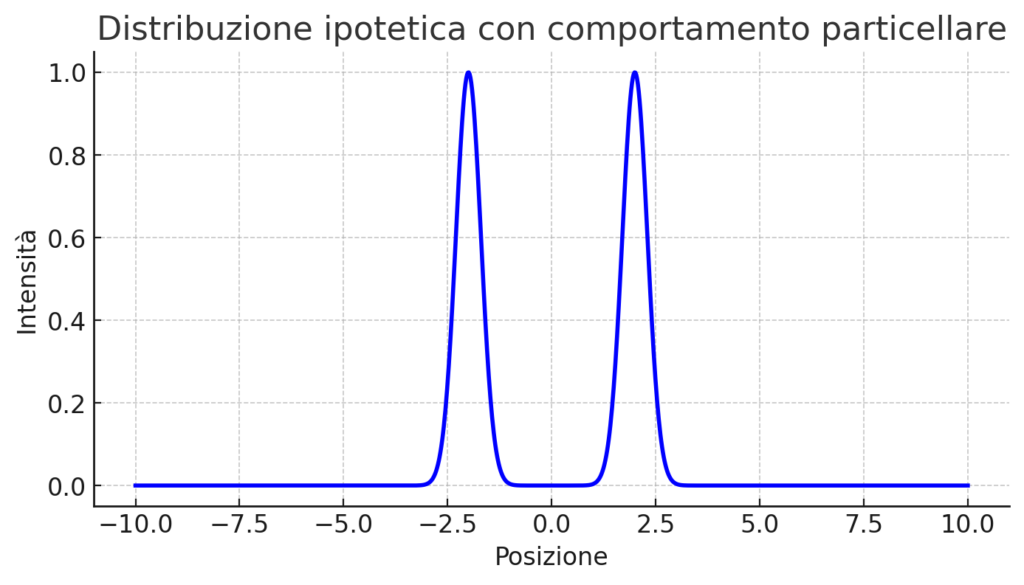
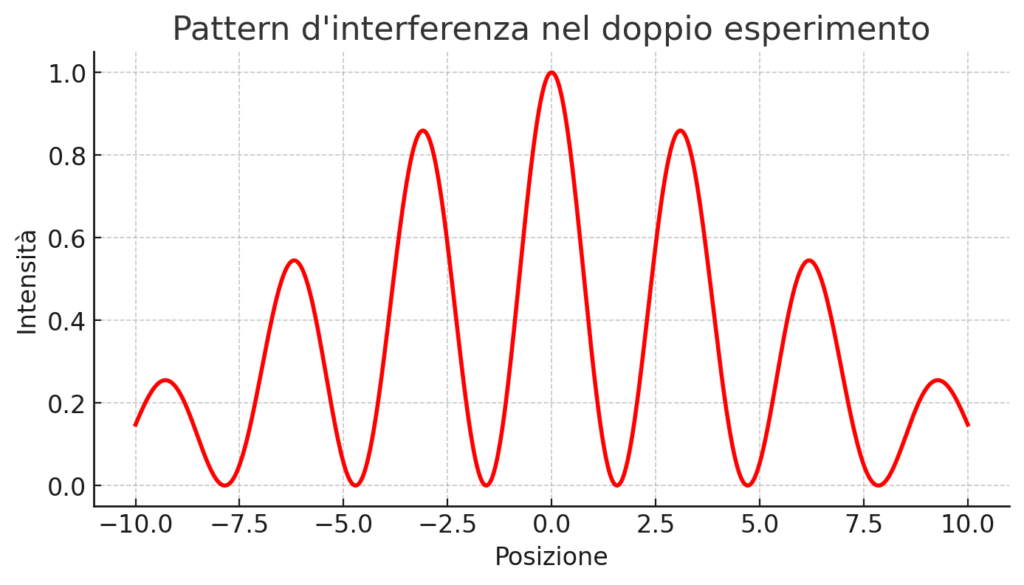
Questo comportamento non è limitato agli elettroni. Anche i fotoni, particelle della luce, mostrano lo stesso fenomeno. La luce, storicamente considerata un’onda, esibisce proprietà corpuscolari nell’effetto fotoelettrico, dove l’energia viene trasferita in quanti discreti. Anche particelle massicce come atomi e molecole dimostrano proprietà ondulatorie in esperimenti avanzati.

Il dualismo onda-particella sfida le nostre categorie percettive tradizionali. Come può un’entità essere allo stesso tempo una particella localizzata e un’onda diffusa? Le particelle quantistiche non sono né onde né particelle nel senso classico, ma entità quantistiche che manifestano entrambe le proprietà a seconda del contesto sperimentale.

Matematicamente, questo comportamento è descritto dalla funzione d’onda, che contiene tutte le informazioni sullo stato di un sistema quantistico. Il modulo quadrato della funzione d’onda fornisce la probabilità di trovare una particella in una certa posizione o con una certa quantità di moto. Questo approccio probabilistico è una delle caratteristiche distintive della meccanica quantistica.

L’equazione di Schrödinger descrive l’evoluzione della funzione d’onda, spiegando come lo stato quantistico di un sistema si modifichi nel tempo e integrando sia gli aspetti ondulatori che particellari. Per sistemi semplici, come l’atomo di idrogeno, le soluzioni evidenziano la quantizzazione delle energie, una conseguenza diretta del comportamento ondulatorio. Un esempio chiave di questo principio è l’elettrone nell’atomo di idrogeno, che si comporta come un’onda stazionaria attorno al nucleo. Questa onda non può assumere qualsiasi forma o energia, ma solo certe configurazioni discrete, simili al comportamento di una corda vibrante. Quando una corda è fissata alle estremità, come in un violino o in una chitarra, le onde che si formano lungo di essa devono rispettare condizioni specifiche: la lunghezza d’onda deve essere tale che l’onda si “chiuda” su se stessa, creando nodi in punti fissi. Solo determinate lunghezze d’onda, e quindi determinate frequenze di vibrazione, sono consentite. In altre parole, la corda può vibrare solo a certe frequenze naturali, dette armoniche, e non può oscillare a frequenze intermedie.

Allo stesso modo, l’elettrone nell’atomo si comporta come un’onda stazionaria che può “adattarsi” attorno al nucleo solo in certi modi specifici. Le configurazioni d’onda consentite sono associate a livelli energetici discreti, o quantizzati, esattamente come le armoniche della corda vibrante. Questo significa che l’elettrone non può assumere energie qualsiasi, ma solo valori ben definiti, determinati dalle soluzioni dell’equazione di Schrödinger.

Il dualismo onda-particella ha implicazioni filosofiche e pratiche. Filosoficamente, ci costringe a riconsiderare la natura della realtà: se le particelle esistono in una sovrapposizione di stati fino al momento della misurazione, il mondo è intrinsecamente probabilistico e indeterminato, mettendo in discussione il determinismo classico.

Praticamente, il dualismo è alla base di molte tecnologie moderne. I microscopi elettronici sfruttano la natura ondulatoria degli elettroni per ottenere immagini ad altissima risoluzione. I laser manipolano fotoni coerenti, e la comprensione dei semiconduttori, cruciale per l’elettronica moderna, deriva dai principi quantistici.

Il dualismo non rappresenta una contraddizione, ma una forma di complementarità. Niels Bohr formulò il principio di complementarità, secondo cui le proprietà quantistiche, come il comportamento ondulatorio o corpuscolare, non si escludono a vicenda, ma emergono in base al contesto dell’osservazione. La natura di una particella non è assoluta, ma dipende dall’apparato sperimentale e dalle misurazioni effettuate. Possiamo progettare esperimenti per rivelarne il carattere particellare e modificarli per mettere in evidenza la sua natura ondulatoria, dimostrando così che entrambe le descrizioni sono aspetti inseparabili della stessa realtà.

Comprendere questo principio ci ha permesso di approfondire la nostra conoscenza del mondo quantistico e di sviluppare tecnologie innovative che hanno trasformato la nostra vita quotidiana. Esso è un invito ad ampliare i nostri orizzonti mentali, in modo da iniziare ad apprezzare la bellezza intrinseca dell’universo a livello fondamentale.

3.2 Il Principio di Sovrapposizione

Il principio di sovrapposizione è uno dei cardini della meccanica quantistica e rappresenta una netta distinzione rispetto alla fisica classica. Secondo questo principio, un sistema quantistico può trovarsi in una combinazione di più stati contemporaneamente, fino a quando un’osservazione non costringe il sistema a “sceglierne” uno. Per quanto controintuitivo, questo concetto è essenziale per comprendere la natura probabilistica della teoria quantistica e molti dei suoi fenomeni più sorprendenti.

Nel mondo macroscopico, siamo abituati a oggetti che possiedono stati ben definiti: una lampadina è accesa o spenta, un gatto è vivo o morto. A livello quantistico, invece, una particella può esistere in una sovrapposizione di stati, combinando simultaneamente diverse proprietà come posizione, energia o spin.

Un’analogia utile per visualizzare questo fenomeno è l’esperimento mentale della moneta quantistica. Immaginiamo una moneta che, invece di mostrare solo “testa” o “croce”, esista in una sovrapposizione di entrambi gli stati. Finché non viene osservata, la moneta non è né testa né croce, ma una combinazione di entrambe le possibilità. Solo al momento della misurazione assume definitivamente uno dei due valori, con una probabilità determinata.

Questo comportamento non è dovuto a una nostra ignoranza dello stato della moneta o a limiti nella misurazione, ma è una proprietà intrinseca del mondo quantistico. Prima dell’osservazione, la moneta non possiede un valore definito: esiste in uno stato di sovrapposizione. Questo aspetto, così distante dalla nostra esperienza quotidiana, impone una revisione radicale delle intuizioni con cui interpretiamo la realtà.

Matematicamente, il principio di sovrapposizione è descritto attraverso la funzione d’onda, che racchiude tutte le informazioni sullo stato quantistico di un sistema. Utilizzando il formalismo di Dirac, uno stato quantistico può essere rappresentato come un vettore |ψ⟩ nello spazio di Hilbert. Se uno stato quantistico può essere in due stati base |α⟩ e |β⟩, la sovrapposizione è data da:

\( |ψ⟩ = c_1 |α⟩ + c_2 |β⟩\)

dove c1​ e c2 sono coefficienti complessi che determinano le ampiezze di probabilità dei rispettivi stati. Il modulo quadrato di questi coefficienti,

\(|c_1|^2 \ e \ |c_2|^2\)

fornisce la probabilità di trovare il sistema in uno dei due stati al momento della misurazione.

Un altro modo per comprendere la sovrapposizione è attraverso l’esperimento del gatto di Schrödinger. Immaginiamo un gatto chiuso in una scatola con un meccanismo che ha il 50% di probabilità di ucciderlo in base al decadimento di una particella radioattiva. Fino a quando non apriamo la scatola, il gatto esiste in una sovrapposizione di “vivo” e “morto”. Questo paradosso evidenzia come l’applicazione dei principi quantistici al mondo macroscopico generi situazioni apparentemente assurde, che richiedono una revisione del nostro modo di interpretare la realtà.

È importante notare che la sovrapposizione non implica che le proprietà fisiche siano indeterminate o confuse, ma che coesistono come possibilità reali fino alla misurazione. Questo introduce un elemento di indeterminazione nella natura, che non dipende da mancanza di conoscenza ma è una caratteristica intrinseca della meccanica quantistica.

Il collasso della funzione d’onda avviene nel momento della misurazione, quando la sovrapposizione si riduce a uno stato definito, con una probabilità determinata dalle ampiezze della funzione d’onda. Questo processo solleva questioni filosofiche sul ruolo dell’osservatore e sulla natura della realtà.

La decoerenza quantistica fornisce una spiegazione fondamentale del motivo per cui nel mondo macroscopico non osserviamo oggetti in stati di sovrapposizione, come nel celebre paradosso del gatto di Schrödinger. Nel dominio quantistico, un sistema isolato può esistere in una sovrapposizione di stati, il che significa che può assumere più configurazioni contemporaneamente fino a quando non viene misurato. Tuttavia, nel mondo reale, i sistemi non sono mai completamente isolati: interagiscono costantemente con l’ambiente circostante, che può essere costituito da molecole d’aria, radiazioni, vibrazioni termiche o persino campi elettromagnetici. Queste interazioni con l’ambiente esterno agiscono come una sorta di “misurazione continua”, che distrugge la sovrapposizione degli stati quantistici molto rapidamente, in funzione della scala, rendendo la transizione al mondo classico inevitabile. In altre parole, il processo di decoerenza impedisce la persistenza di stati sovrapposti su scale macroscopiche.

Nel caso del gatto di Schrödinger, il motivo per cui non abbiamo un gatto contemporaneamente vivo e morto è che il sistema “gatto + ambiente” è estremamente complesso e interagisce con un numero sterminato di particelle circostanti. La decoerenza avviene quasi istantaneamente, forzando il gatto a trovarsi in uno stato ben definito (vivo o morto) molto prima che un osservatore apra la scatola. In altre parole, non è necessario il “collasso” della funzione d’onda tramite un’osservazione consapevole: la stessa interazione con l’ambiente è sufficiente a far emergere la realtà classica.

Questa spiegazione elimina l’apparente assurdità del paradosso, mostrando che la sovrapposizione è un fenomeno che si manifesta solo su scala atomica, dove la decoerenza è trascurabile. Negli esperimenti quantistici in laboratorio, per mantenere stati di sovrapposizione, è necessario isolare il sistema dall’ambiente esterno, cosa impossibile su scala macroscopica.

Accettare il principio di sovrapposizione richiede un cambiamento di prospettiva: dobbiamo abbandonare l’idea che le proprietà di un sistema atomico o subatomico siano sempre definite indipendentemente dalla misurazione. La natura può esistere in uno stato di possibilità fino a che non viene osservata. Questo non rende la meccanica quantistica illogica; essa segue leggi matematiche precise che descrivono accuratamente il comportamento dei sistemi a livello fondamentale.

Il principio di sovrapposizione è cruciale per comprendere la meccanica quantistica. Ci invita a espandere le nostre categorie mentali e ad accettare che la realtà a livello fondamentale possa differire dalla nostra esperienza quotidiana. Riconoscendo la coerenza della teoria quantistica, possiamo apprezzare come le sue apparenti stranezze riflettano un cambiamento necessario nella nostra concezione della realtà.

3.3 Quantizzazione dell’Energia

La quantizzazione dell’energia è un altro dei concetti basilari della meccanica quantistica e ha rivoluzionato la nostra comprensione del mondo microscopico. A differenza della fisica classica, dove l’energia può assumere valori continui, La meccanica quantistica stabilisce che l’energia, in numerosi contesti, non può variare in modo continuo, ma assume valori discreti, o ‘quantizzati’. Le particelle possono quindi possedere solo energie specifiche, e le transizioni tra questi livelli avvengono attraverso “salti quantici” piuttosto che cambiamenti continui.

Il concetto di quantizzazione dell’energia fu introdotto da Max Planck nel 1900, durante lo studio della radiazione del corpo nero, un problema che la fisica classica non riusciva a spiegare. La radiazione del corpo nero è l’emissione elettromagnetica di un oggetto ideale che assorbe tutta la radiazione incidente, emettendo radiazione solo in base alla sua temperatura. La fisica classica prevedeva che l’intensità della radiazione aumentasse all’infinito per alte frequenze (la cosiddetta “catastrofe ultravioletta”), ma questo non accadeva sperimentalmente. Planck risolse il problema ipotizzando che l’energia fosse emessa o assorbita in pacchetti discreti chiamati quanti, proporzionali alla frequenza della radiazione, secondo la relazione:

\( E = h \nu \)

dove h è la costante di Planck e ν è la frequenza.

Un esempio significativo di quantizzazione dell’energia è l’atomo di Bohr. Niels Bohr propose che gli elettroni orbitano attorno al nucleo solo in orbite stazionarie con energie quantizzate. Quando un elettrone passa da un’orbita a un’altra, emette o assorbe un fotone con un’energia pari alla differenza tra i due livelli energetici:

\( \Delta E = E_{\text{finale}} – E_{\text{iniziale}} = h \nu \)

Questo modello spiegava con successo le righe spettrali dell’idrogeno, che erano un enigma per la fisica classica. Le linee di emissione e assorbimento osservate negli spettri atomici corrispondono a transizioni tra livelli energetici quantizzati degli elettroni.

Un altro fenomeno chiave che illustra la quantizzazione dell’energia è l’effetto fotoelettrico, per il quale Albert Einstein ricevette il Premio Nobel. Quando la luce colpisce una superficie metallica, può causare l’emissione di elettroni, ma solo se la frequenza della luce supera una certa soglia. Einstein spiegò questo effetto assumendo che la luce fosse composta da fotoni, ciascuno con energia \( E = h \nu \), fornendo ulteriore evidenza della quantizzazione dell’energia.

La quantizzazione si applica a tutti i sistemi quantistici. Un esempio è l’oscillatore armonico quantistico, come una molecola vibrante. L’energia di un oscillatore quantistico è data dalla relazione:

\( E_n = \left( n + \frac{1}{2} \right) \hbar \omega \)

dove n è un numero intero non negativo, h tagliata è la costante di Planck ridotta e omega è la frequenza angolare dell’oscillatore. L’energia è quantizzata e non può mai essere zero, a causa dell’energia di punto zero:

\( \frac{1}{2} \hbar \omega \)

Il formalismo di Dirac esprime in modo conciso gli stati quantistici e le loro energie. Gli stati energetici di un sistema possono essere rappresentati da vettori |n⟩ nello spazio di Hilbert, e l’operatore hamiltoniano

\( \hat{H} \)

rappresenta l’energia totale. L’equazione:

\( \hat{H} |n⟩ = E_n |n⟩ \)

mostra che gli stati |n⟩ sono autostati dell’energia con autovalori En, ossia le energie quantizzate del sistema.

La quantizzazione dell’energia spiega anche fenomeni come l’effetto tunnel, dove una particella ha una probabilità di attraversare una barriera di potenziale più alta della sua energia totale. Questo è possibile grazie alla natura ondulatoria delle particelle. L’effetto tunnel è alla base di dispositivi elettronici come i diodi a tunnel e tecniche di microscopia come il microscopio a effetto tunnel (STM).

La quantizzazione si manifesta nei livelli energetici nucleari e nei processi di decadimento radioattivo. I nuclei atomici hanno livelli energetici quantizzati, e le transizioni tra questi livelli comportano l’emissione o l’assorbimento di particelle come alfa, beta o gamma.

Nel campo della superconduttività, la quantizzazione gioca un ruolo cruciale. Nei circuiti superconduttori, il flusso magnetico è quantizzato in unità di

\( \style{font-size:1em;}{\displaystyle \frac{h}{2e}} \)

con e la carica dell’elettrone.

La quantizzazione ha portato allo sviluppo di tecnologie come i laser, che sfruttano l’emissione stimolata di fotoni tra livelli energetici quantizzati per produrre luce coerente, e i semiconduttori, che utilizzano le bande di energia quantizzate per creare transistor, diodi e circuiti integrati.

Anche i punti quantici, materiali nanostrutturati, esibiscono proprietà determinate dalla quantizzazione dell’energia. I punti quantici, con livelli energetici discreti, hanno applicazioni in display avanzati, fotovoltaico e medicina.

La quantizzazione dell’energia richiede un cambiamento nella nostra comprensione. A livello microscopico, l’energia non è un continuum fluido, ma è composta da valori discreti. Questo concetto spiega fenomeni che la fisica classica non poteva giustificare e rivela una coerenza intrinseca nella natura.

La quantizzazione dell’energia non implica che l’energia non possa cambiare, ma che lo faccia in passi discreti, simile a salire o scendere una scala: si può muovere solo di un gradino alla volta.

La quantizzazione dell’energia permea tutta la fisica quantistica. Comprendere questo concetto ci permette di apprezzare come la natura operi secondo leggi che, sebbene diverse dalle nostre intuizioni, sono logiche e coerenti. Questo principio spiega fenomeni atomici e nucleari e ha dato vita a tecnologie avanzate, dimostrando come accettare nuovi paradigmi ci consenta di progredire e innovare.

3.4 Il Collasso della Funzione d’Onda

Il collasso della funzione d’onda è uno dei concetti più discussi e affascinanti della meccanica quantistica. Esso descrive il processo attraverso cui una particella quantistica passa da uno stato di sovrapposizione a uno stato definito a seguito di una misurazione. Questo concetto è strettamente legato al ruolo dell’osservazione e solleva domande profonde sulla natura della realtà e sul significato dell’atto di misurare.

Secondo il principio di sovrapposizione, un sistema quantistico può esistere in una combinazione di stati possibili fino al momento della misurazione. La funzione d’onda Ψ (Psi), che descrive lo stato quantistico del sistema, racchiude le probabilità di trovare la particella in vari stati. Questa funzione evolve in modo deterministico secondo l’equazione di Schrödinger:

\( \style{font-size:1em;}{i\hbar \frac{\partial}{\partial t} |\Psi(t)\rangle = \hat{H} |\Psi(t)\rangle} \)

fintanto che non viene effettuata alcuna misurazione.

Tuttavia, al momento della misurazione, la funzione d’onda sembra “collassare” in uno degli autostati dell’osservabile misurata, e il sistema assume un valore definito per quella proprietà. Questo fenomeno è il collasso della funzione d’onda.

Per chiarire, consideriamo un elettrone in una sovrapposizione di stati di spin “su” e “giù”. Il suo stato può essere descritto come:

\( |\Psi⟩ = c_{\uparrow} |\uparrow⟩ + c_{\downarrow} |\downarrow⟩ \)

dove

\( \style{font-size:1em;}{\displaystyle |\uparrow\rangle \quad e \quad |\downarrow\rangle}\)

sono gli autostati di spin, e

\( \style{font-size:1em;}{\displaystyle c_{\uparrow} \quad e \quad c_{\downarrow}} \)

sono coefficienti complessi che determinano le probabilità associate. Prima della misurazione, l’elettrone esiste in una sovrapposizione di questi stati. Quando si misura lo spin, la funzione d’onda collassa in uno di essi e l’elettrone assume un valore definito.

Il collasso della funzione d’onda ha portato alle seguenti diverse interpretazioni della meccanica quantistica di cui solo la prima è largamente accettata:

1. Interpretazione di Copenaghen: Sostiene che il collasso avviene durante la misurazione, e lo stato quantistico non ha senso prima dell’osservazione in termini definiti.
2. Interpretazione a Molti Mondi: Suggerisce che non ci sia un vero collasso; tutte le possibilità si realizzano in universi paralleli.
3. Interpretazione a Variabili Nascoste: Propone l’esistenza di variabili non osservabili che determinano l’esito delle misurazioni, rendendo il sistema deterministico.
4. Interpretazione Relazionale: Vede lo stato quantistico come relativo all’osservatore e il collasso come un aggiornamento delle informazioni sull’osservabile.

Il ruolo dell’osservazione è cruciale. Spesso si dibatte se sia necessaria una coscienza per provocare il collasso o se basti l’interazione con l’ambiente. La teoria della decoerenza quantistica, decritta in precedenza, fornisce una spiegazione alternativa, suggerendo che le interazioni con l’ambiente provocano una perdita di coerenza tra gli stati sovrapposti, portando al comportamento classico senza la necessità di un osservatore cosciente.

Il collasso della funzione d’onda ha applicazioni pratiche significative. Nella crittografia quantistica, per esempio, il principio che l’osservazione altera lo stato di un sistema quantistico garantisce la sicurezza delle comunicazioni: qualsiasi tentativo di intercettazione è rilevabile. Nei computer quantistici, il collasso rappresenta una sfida, poiché la coerenza quantistica è essenziale per il funzionamento dei qubit in sovrapposizione, ma è necessario per leggere i risultati.

Nonostante la sua apparente stranezza, il collasso della funzione d’onda non viola le leggi fondamentali della fisica. In molte interpretazioni, rappresenta un cambiamento nella conoscenza dell’osservatore, piuttosto che una trasformazione fisica istantanea nel sistema. Questo approccio suggerisce che la funzione d’onda non descrive la realtà oggettiva, ma la nostra conoscenza di essa.

Il collasso della funzione d’onda ci costringe a rivedere il concetto di realismo. Se le proprietà fisiche non si manifestano fino al momento della misurazione, la realtà quantistica assume una natura intrinsecamente probabilistica, sfidando il realismo classico, che presuppone l’esistenza indipendente delle proprietà degli oggetti.

Accettare il collasso della funzione d’onda richiede un definitivo e radicale cambio di prospettiva: dobbiamo abbandonare l’idea di un universo deterministico, in cui tutto è definito in ogni istante, e accogliere l’idea che la realtà a livello quantistico sia governata dalla probabilità e che l’osservazione giochi un ruolo cruciale nel determinare i fenomeni.

Sebbene controintuitivo, il collasso della funzione d’onda segue una logica interna coerente, riflettendo la natura probabilistica del mondo quantistico e l’importanza dell’osservazione o dell’interazione con l’ambiente nel definire lo stato finale di un sistema. Comprendere questo concetto ci offre una visione più profonda della realtà, invitandoci a esplorare paradigmi che vanno oltre le nostre intuizioni basate sul mondo macroscopico.

3.5 L’Entanglement

L’entanglement quantistico, o intreccio quantistico, è uno dei fenomeni più misteriosi della meccanica quantistica. Esso descrive una situazione in cui due o più particelle diventano così strettamente correlate che lo stato di una non può essere descritto indipendentemente dallo stato dell’altra, anche se distanti tra loro. L’entanglement sfida le nostre intuizioni su come dovrebbero comportarsi le proprietà fisiche e ha implicazioni profonde sia teoriche che pratiche.

Nel mondo macroscopico, immaginiamo correlazioni semplici. Se lanciamo due monete, il risultato di una non influenza l’altra. Se, però, le monete fossero truccate per mostrare sempre risultati opposti, avremmo una correlazione perfetta: se una moneta mostra “testa”, l’altra mostrerà sicuramente “croce”.

Nel mondo quantistico, tuttavia, le correlazioni sono più profonde. Immaginiamo due particelle, ad esempio due elettroni, in uno stato entangled. Le loro proprietà, come lo spin, sono correlate in modo che la misurazione dello spin di una particella determini immediatamente lo spin dell’altra, anche se distanti. Se misuriamo lo spin di una particella e troviamo “su”, sappiamo subito che l’altra particella avrà spin “giù”, e viceversa.

Questo fenomeno sembra violare il principio di località, secondo cui un oggetto può essere influenzato solo da eventi nel suo intorno immediato. La possibilità che una misurazione su una particella influenzi istantaneamente un’altra particella distante ha sollevato importanti questioni. Albert Einstein, con Boris Podolsky e Nathan Rosen, sollevò il famoso paradosso EPR, suggerendo che l’entanglement indicava un’incompletezza della meccanica quantistica.

Gli esperimenti di Alain Aspect, condotti negli anni ’80, hanno confermato che l’entanglement quantistico è un fenomeno reale e che non può essere spiegato con le leggi della fisica classica. Per verificarlo, gli scienziati hanno generato coppie di fotoni entangled, cioè particelle di luce che, pur essendo separate, restano in uno stato di correlazione. Ogni fotone veniva inviato in una direzione diversa e analizzato in due laboratori distinti. La particolarità dell’esperimento stava nel fatto che gli strumenti di misura cambiavano impostazione all’ultimo momento, quando i fotoni erano già in viaggio. Questo eliminava la possibilità che le particelle potessero “decidere” in anticipo il loro comportamento sulla base di una proprietà nascosta.

Un esempio utile per illustrare questo fenomeno è quello delle particelle gemelle. Immaginiamo una sorgente che emetta coppie di fotoni entangled, le cui polarizzazioni siano correlate. Se due osservatori distanti, Alice e Bob, misurano la polarizzazione di questi fotoni, scopriranno che i loro risultati sono sempre perfettamente legati tra loro. Se Alice trova che il suo fotone è polarizzato verticalmente, Bob misurerà automaticamente una polarizzazione orizzontale, e viceversa. Questo accade indipendentemente dalla distanza tra i due, suggerendo che le proprietà dei fotoni non fossero già determinate in anticipo, ma che il loro stato si definisse solo al momento della misurazione.

I risultati degli esperimenti di Aspect hanno dimostrato che, nonostante la separazione spaziale, i fotoni continuavano a rispondere alle misurazioni in modo coerente, come se comunicassero istantaneamente tra loro. Questo comportamento violava le disuguaglianze di Bell, un test matematico progettato per verificare se l’entanglement potesse essere spiegato da variabili nascoste locali. Il superamento di questo limite imponeva di accettare che la meccanica quantistica descrivesse correttamente la realtà, anche se in un modo profondamente diverso da quello a cui siamo abituati.

Tuttavia, l’entanglement non consente la trasmissione di informazioni a velocità superiori a quella della luce. Le misurazioni sui singoli sistemi entangled producono risultati casuali, e solo confrontando i dati a posteriori è possibile rilevare le correlazioni. Questo fenomeno, che Einstein definì “azione spettrale a distanza”, non viola la relatività speciale, poiché non implica un trasferimento istantaneo di informazione utilizzabile.

Per capire meglio come l’entanglement non violi causalità o relatività, dobbiamo accettare che le proprietà delle particelle entangled non sono definite fino alla misurazione. La funzione d’onda entangled descrive il sistema nel suo insieme, non le particelle individualmente. In questo senso, le particelle entangled non sono entità indipendenti, ma parte di un unico sistema quantistico.

Matematicamente, uno stato entangled può essere rappresentato attraverso il formalismo di Dirac. Consideriamo due particelle con spin 1/2, come gli elettroni, in uno stato entangled di spin singoletto:

\( \style{font-size:1em;}{\displaystyle |\Psi\rangle = \frac{1}{\sqrt{2}} \left( |\uparrow\rangle_A |\downarrow\rangle_B – |\downarrow\rangle_A |\uparrow\rangle_B \right)} \)

Le particelle A e B non hanno spin definiti individualmente, ma il sistema nel suo insieme ha spin totale zero. Le misurazioni degli spin saranno sempre anticorrelate: se A ha spin “su”, B avrà spin “giù”.

L’entanglement non è limitato a coppie di particelle, ma può coinvolgere più sistemi, dando origine a stati complessi. Questo fenomeno è fondamentale per la computazione quantistica e la crittografia quantistica.

Nei computer quantistici, l’entanglement permette ai qubit di eseguire calcoli in parallelo grazie alla sovrapposizione di stati e alle correlazioni entangled. Questo potenziale di calcolo esponenziale supera di gran lunga i computer classici in problemi specifici, come la fattorizzazione di grandi numeri e la simulazione di sistemi quantistici.

Nella crittografia quantistica, l’entanglement garantisce chiavi crittografiche assolutamente sicure. Protocolli come BB84 o E91 sfruttano l’entanglement per rilevare eventuali intercettazioni, poiché qualsiasi tentativo di misurazione altera lo stato del sistema, segnalando la violazione.

L’entanglement ha implicazioni filosofiche profonde. Sfida le nozioni classiche di separabilità e indipendenza, suggerendo che la realtà a livello quantistico è più interconnessa di quanto possiamo immaginare. Nonostante la sua stranezza, l’entanglement non viola le leggi fondamentali della fisica, poiché le correlazioni non possono essere utilizzate per comunicare istantaneamente.

L’entanglement non è solo un fenomeno teorico, ma è attivamente studiato per comprendere meglio la gravità quantistica e la struttura dell’universo. Alcuni fisici ipotizzano che lo spazio-tempo stesso possa emergere da stati entangled, suggerendo una connessione tra entanglement e la geometria dell’universo.

L’entanglement è un fenomeno centrale della meccanica quantistica che, sebbene sfidi le nostre intuizioni, segue una logica coerente nel quadro quantistico. Estendendo le nostre categorie mentali, possiamo apprezzare la profondità di questo fenomeno, che ci offre nuove prospettive sulla natura della realtà e apre la strada a tecnologie rivoluzionarie.

Capitolo 4: Esperimenti Mentali Originali

4.1 Principio di Indeterminazione:

Il disegno che si sfoca nel momento in cui lo osservi troppo da vicino

Immagina un supporto su cui è impresso un disegno, la cui nitidezza rimane inalterata solo quando osservato da una distanza specifica. Nel momento in cui avvicini per esaminare i dettagli con maggiore precisione, il calore del tuo respiro o il semplice atto di focalizzarti su un punto specifico provoca l’alterazione dell’inchiostro, rendendo l’immagine sfocata e indistinta. Più tenti di cogliere i dettagli con accuratezza, più l’insieme diventa confuso. Per ottenere una conoscenza esatta di un elemento specifico, è necessario sacrificare la visione d’insieme, mentre per mantenere una prospettiva globale bisogna rinunciare alla precisione dei dettagli. Questa tensione continua tra risoluzione e ampiezza di visione riflette direttamente il principio di indeterminazione di Heisenberg.

Tale principio postula che esiste un limite fondamentale alla precisione con cui si possono misurare simultaneamente due grandezze coniugate, come la posizione e la quantità di moto di una particella. Il processo di misura stesso introduce un’alterazione irreversibile nel sistema, impedendo di determinare con assoluta precisione entrambe le variabili contemporaneamente. Questo fenomeno ha profonde implicazioni sulla natura della realtà fisica, ponendo interrogativi fondamentali sulla natura dell’osservazione e sul ruolo del soggetto misurante.

La relazione di indeterminazione ha conseguenze dirette sulla struttura dei livelli energetici nei sistemi quantistici confinati, come negli atomi, e sul comportamento delle particelle elementari negli acceleratori. Il principio è alla base dell’instabilità quantistica e della necessità di una descrizione probabilistica dei fenomeni microscopici.

4.2 Dualismo Onda-Particella:

La melodia trasformata in sassi

Consideriamo la propagazione di un’onda sonora: una melodia che si diffonde nello spazio come un’onda continua e armoniosa, descrivibile matematicamente attraverso una funzione d’onda che evolve nel tempo secondo l’equazione di Schrödinger. Finché la si ascolta senza tentare di isolarne un singolo elemento, il suono mantiene il suo carattere diffuso e distribuito. Tuttavia, nel momento in cui si cerca di estrarre una singola nota per analizzarla, essa perde la sua natura ondulatoria e si materializza come un’entità discreta, analoga a una particella puntiforme. Invece di percepire la melodia come un flusso armonioso e continuo, sperimenteremmo solo una successione di impulsi isolati, come se il suono non fosse più un’onda avvolgente, ma una serie di minuscoli impatti discreti sull’ambiente e sul nostro corpo.

Questo esperimento mentale è una metafora efficace per descrivere il dualismo onda-particella, secondo il quale entità quantistiche, come elettroni e fotoni, mostrano caratteristiche sia ondulatorie che corpuscolari a seconda del tipo di misura effettuata. Il fenomeno è alla base di esperimenti chiave come la doppia fenditura di Young, che evidenzia la coesistenza di entrambi i comportamenti.

L’onda associata a una particella non è un’onda fisica nel senso classico, ma rappresenta la distribuzione di probabilità di trovare la particella in una determinata regione dello spazio. Questo concetto è alla base dell’interpretazione di Copenaghen della meccanica quantistica, in cui il ruolo dell’osservatore è cruciale nel determinare il comportamento del sistema.

4.3 Principio di Sovrapposizione:

L’archivio delle storie non scritte

Immagina un vasto archivio pieno di volumi ancora chiusi, ognuno contenente una storia che non è stata ancora letta. Finché nessuno sfoglia una pagina, ogni libro racchiude infinite trame possibili, tutte coesistenti in uno stato di sovrapposizione. Ma nel momento in cui scegli di aprirne uno e iniziare a leggere, la storia si cristallizza in un’unica versione, mentre tutte le altre possibilità svaniscono, lasciando spazio a una sola narrazione definitiva.

Questo principio è centrale nella meccanica quantistica: un sistema quantistico può esistere in una combinazione lineare di stati fino a che non viene effettuata una misurazione, la quale forza il sistema a collassare in uno stato determinato. La sovrapposizione è alla base di tecnologie emergenti come il calcolo quantistico, dove i qubit possono esistere in una combinazione simultanea di 0 e 1 fino al momento della lettura.

Nel contesto sperimentale, la sovrapposizione è stata confermata attraverso esperimenti di interferenza e correlazioni quantistiche. Il ruolo della decoerenza quantistica è fondamentale per comprendere il modo in cui la sovrapposizione viene distrutta dall’interazione con l’ambiente esterno, portando alla transizione verso il comportamento classico.

4.4 Collasso della Funzione d’Onda:

Il labirinto che cambia mentre lo attraversi

Immagina un labirinto in cui tutte le possibili strade coesistono simultaneamente. Ogni percorso è accessibile fino a che non scegli una direzione. Tuttavia, nel momento in cui prendi una decisione e ti muovi in una direzione specifica, tutte le altre opzioni scompaiono, lasciandoti con un’unica possibilità determinata.

Questa immagine rende intuitivo il concetto di collasso della funzione d’onda: un sistema quantistico, descritto inizialmente da una sovrapposizione di stati, si riduce a uno stato unico al momento della misurazione. Il collasso è uno degli aspetti più dibattuti dell’interpretazione della meccanica quantistica, con implicazioni sulla natura stessa della realtà.

L’interpretazione a molti mondi di Everett propone un’alternativa al collasso, suggerendo che tutti gli stati possibili continuano a esistere in universi paralleli, eliminando la necessità di una riduzione della funzione d’onda.

4.5 Entanglement:

L’Intreccio Invisibile di Due Amici

Immagina due giovani amici inseparabili, con un legame così profondo da influenzarsi a vicenda in modo spontaneo e immediato. Ogni volta che uno di loro è triste, l’altro trova sempre il modo di tirarlo su di morale. Non è necessario che parlino: il semplice sapere che l’altro c’è, pronto a portare luce nei momenti bui, è sufficiente per ristabilire un equilibrio.

Poi, un giorno, la vita li separa. Vivono in città diverse, forse addirittura in continenti lontani. Eppure, qualcosa di straordinario accade: ogni volta che uno di loro si sente giù, sa istintivamente che l’amico, lontano, sta vivendo un momento di gioia. E proprio questa consapevolezza lo aiuta a sentirsi meglio, come se la felicità dell’altro fosse sempre a sua disposizione. Nessuno dei due deve inviare messaggi o fare telefonate: il loro legame funziona a distanza, in modo istantaneo.

Questo è il cuore dell’entanglement quantistico. Due particelle intrecciate si influenzano reciprocamente, indipendentemente dalla distanza che le separa. Quando una assume uno stato, l’altra risponde immediatamente, senza bisogno di segnali visibili. Come gli amici del nostro esperimento mentale, queste particelle non “comunicano” nel senso classico, ma sono parte di un’unica realtà condivisa, in cui la misura di una determina istantaneamente lo stato dell’altra.

Nel mondo quantistico, il concetto di separazione è solo un’illusione: ciò che è stato unito una volta rimane connesso per sempre, come due amici che, anche a chilometri di distanza, continuano a sostenersi l’un l’altro in modi misteriosi e profondi.

4.6 Effetto Tunnel Quantistico:

La porta chiusa che puoi attraversare senza aprirla

Immagina di trovarti di fronte a una porta chiusa. Ogni tentativo di attraversarla si scontra con un ostacolo invalicabile: secondo la logica quotidiana, dovresti aprirla per passare. Eppure, in rare occasioni e senza alcuna azione visibile, ti ritrovi dall’altra parte, come se la porta non fosse mai esistita.

Questo è l’effetto tunnel quantistico: una particella può superare una barriera energetica che, secondo la fisica classica, dovrebbe bloccarla. Non sfonda, non la aggira, ma la attraversa come se fosse un’ombra.

Questo fenomeno è fondamentale in molteplici contesti, dalla dinamica nucleare ai processi astrofisici, fino alla tecnologia dei semiconduttori. Senza l’effetto tunnel, il Sole non brillerebbe e i microchip non funzionerebbero. Ci mostra che, nel regno quantistico, l’impossibile a volte è solo un’illusione.

Appendice 1: Il ruolo della filosofia nella fisica quantistica

La fisica quantistica, con la sua struttura matematica sofisticata e le implicazioni che sfidano l’intuizione, ha aperto un fertile terreno di dibattito filosofico. Le sue fondamenta probabilistiche, il ruolo dell’osservatore e la ridefinizione dei concetti di realtà, causalità e determinismo sollevano questioni epistemologiche e ontologiche di grande rilievo. Questo intreccio tra fisica e filosofia ha generato una riflessione continua, contribuendo a una comprensione più profonda della natura ultima della realtà. Tuttavia, questa interazione non si limita a questioni accademiche astratte, ma influisce direttamente sulla formulazione e interpretazione dei modelli fisici, sulla loro applicabilità e sulle possibilità di estensione teorica verso nuovi paradigmi scientifici.

Il Problema dell’Interpretazione

Uno dei nodi centrali della filosofia della fisica riguarda l’interpretazione della meccanica quantistica. Sebbene la teoria fornisca previsioni empiriche estremamente accurate, il significato di tali risultati rimane oggetto di discussione. L’Interpretazione di Copenaghen, proposta da Niels Bohr e Werner Heisenberg, introduce il principio di complementarità e sostiene che le proprietà quantistiche non assumano valori definiti prima della misurazione. Questo porta a un’indagine sul ruolo epistemologico dell’osservatore e sul significato stesso della realtà fisica. Ma il concetto di complementarità solleva anche interrogativi riguardo alla natura del linguaggio scientifico: fino a che punto possiamo descrivere il mondo quantistico utilizzando i termini della fisica classica? Questo limite concettuale impone un ripensamento del realismo scientifico e delle metodologie con cui si costruisce la conoscenza.

In alternativa, l’Interpretazione a Molti Mondi di Hugh Everett elimina la necessità del collasso della funzione d’onda, suggerendo che ogni possibile stato quantistico si realizzi in un universo parallelo. Questa prospettiva solleva interrogativi di carattere metafisico e filosofico sulla natura della realtà e sull’identità personale, mettendo in discussione i concetti tradizionali di determinismo e unicità dell’esperienza. La possibilità che esistano infiniti universi in cui ciascun evento quantistico segue un percorso differente ha portato a una rivalutazione della causalità e della temporalità, con implicazioni che si estendono oltre la fisica teorica e toccano la filosofia del tempo e della coscienza.

Realismo e Antirealismo

Il dibattito tra realismo e antirealismo è uno degli snodi concettuali centrali della filosofia della fisica quantistica. I realisti ritengono che gli enti quantistici, come la funzione d’onda e le particelle subatomiche, abbiano un’esistenza indipendente dall’osservazione. Gli antirealisti, invece, sostengono che tali entità siano costrutti matematici utili per la previsione dei fenomeni, ma privi di una corrispondenza ontologica diretta con la realtà.

L’esperimento dell’entanglement quantistico e la violazione delle disuguaglianze di Bell hanno ulteriormente complicato questa dicotomia, suggerendo che la realtà fisica non possa essere descritta da un modello locale e deterministico. L’interconnessione tra particelle, indipendentemente dalla distanza, ha portato alcuni filosofi a proporre modelli olistici della realtà, nei quali le proprietà quantistiche non sono definite in modo assoluto, ma emergono in relazione al sistema osservato. Questo ha stimolato lo sviluppo di nuove interpretazioni che si discostano dalle classiche dicotomie tra realismo e antirealismo, cercando un’integrazione tra le due prospettive.

Il Ruolo dell’Osservatore

Uno dei più grandi enigmi della meccanica quantistica riguarda il ruolo dell’osservatore. Il principio del collasso della funzione d’onda implica che la misurazione influenzi direttamente lo stato del sistema, sollevando interrogativi sulla natura della conoscenza scientifica e sul rapporto tra mente e realtà fisica. Alcune ipotesi speculative suggeriscono che la coscienza giochi un ruolo attivo nella determinazione degli esiti quantistici, portando il dibattito al confine tra fisica e filosofia della mente. Il tentativo di correlare la coscienza con il collasso della funzione d’onda ha dato origine a numerosi modelli teorici, alcuni dei quali si spingono fino a ipotizzare che la coscienza stessa possa essere un fenomeno quantistico.

Un’interpretazione alternativa è fornita dalla teoria della decoerenza, che descrive la transizione dal comportamento quantistico a quello classico come risultato dell’interazione con l’ambiente. Questo approccio mira a riformulare il problema dell’osservazione in termini di processi fisici oggettivi, senza la necessità di un osservatore cosciente. Tuttavia, il significato profondo della misurazione quantistica rimane un tema aperto di discussione.

Causalità e Determinismo

La meccanica quantistica introduce una forma di indeterminismo intrinseco che si discosta radicalmente dalla visione deterministica della fisica classica. Le leggi quantistiche permettono di calcolare solo la probabilità degli esiti di un esperimento, senza fornire una predizione certa del risultato specifico. Questo ha implicazioni non solo per la fisica, ma anche per la filosofia della causalità e del libero arbitrio. L’indeterminismo quantistico sembra suggerire un modello di causalità probabilistica, nel quale il concetto stesso di causa-effetto deve essere reinterpretato.

La Necessità di un Approccio Interdisciplinare

La fisica quantistica solleva questioni di natura epistemologica, ontologica ed etica che richiedono un dialogo costante tra scienza e filosofia. La filosofia aiuta a chiarire le implicazioni concettuali delle teorie fisiche, mentre la fisica fornisce un quadro matematico ed empirico per guidare la riflessione speculativa. Un approccio interdisciplinare risulta essenziale per affrontare le sfide cognitive e metodologiche poste dalla meccanica quantistica e per comprendere la realtà in modo più profondo e sistematico. Il dialogo tra le due discipline non è solo utile, ma necessario per sviluppare modelli interpretativi capaci di rendere conto delle anomalie e delle apparenti contraddizioni che emergono nello studio della fisica quantistica.

Infine, l’evoluzione delle tecnologie basate su principi quantistici, come il calcolo quantistico e le telecomunicazioni quantistiche, rende ancora più urgente una comprensione filosofica approfondita. Il modo in cui comprendiamo e interpretiamo il mondo quantistico non è solo un problema accademico, ma ha ripercussioni dirette sulla costruzione della conoscenza e sulle applicazioni pratiche della scienza moderna.

Appendice 2 : Introduzione al Formalismo Matematico

Il formalismo di Dirac in parole semplici

La meccanica quantistica, per descrivere il comportamento delle particelle subatomiche, richiede un linguaggio matematico capace di catturare le sue complessità. Uno degli strumenti più eleganti a questo scopo è il formalismo di Dirac, noto anche come notazione bra-ket, introdotto da Paul Dirac. Questo formalismo permette di esporre in modo conciso gli stati quantistici e le osservabili fisiche, semplificando sia la comprensione teorica che i calcoli.

In meccanica quantistica, lo stato di un sistema è descritto da una funzione d’onda che esprime le probabilità di vari risultati, invece di fornire certezze come accade in meccanica classica. Nel formalismo di Dirac, lo stato quantistico viene indicato da un ket, scritto \(\style{font-size:1em;}{\displaystyle | \psi \rangle}\). Ad esempio, lo stato di un elettrone con spin “su” è \(\style{font-size:1em;}{\displaystyle | \uparrow \rangle}\), mentre con spin “giù” è \(\style{font-size:1em;}{\displaystyle | \downarrow \rangle}\). Questi ket sono vettori in uno spazio di Hilbert, un concetto matematico che generalizza gli spazi vettoriali usati in algebra lineare.

L’operazione complementare al ket è il bra, indicato come \(\style{font-size:1em;}{\displaystyle \langle \phi |}\). Il bra viene impiegato per calcolare i prodotti scalari tra stati quantistici, come \(\style{font-size:1em;}{\displaystyle \langle \phi | \psi \rangle}\), il cui modulo quadrato esprime la probabilità di trovare il sistema nello stato \(\style{font-size:1em;}{\displaystyle | \phi \rangle}\) se inizialmente esso si trova nello stato \(\style{font-size:1em;}{\displaystyle | \psi \rangle}\).

La meccanica quantistica consente di combinare stati diversi tramite la sovrapposizione lineare. Se \(\style{font-size:1em;}{\displaystyle | \psi_1 \rangle}\) e \(\style{font-size:1em;}{\displaystyle | \psi_2 \rangle}\) sono due possibili stati, la loro combinazione \(\style{font-size:1em;}{\displaystyle | \psi \rangle = c_1 | \psi_1 \rangle + c_2 | \psi_2 \rangle}\) descrive uno stato valido del sistema. Questo esprime il principio di sovrapposizione, che consente a un sistema di esistere contemporaneamente in più stati fino al momento della misurazione.

Le osservabili, come posizione, energia o spin, sono espresse tramite operatori lineari. Un operatore \(\style{font-size:1em;}{\displaystyle \hat{O}}\) agisce su uno stato \(\style{font-size:1em;}{\displaystyle | \psi \rangle}\) per produrre un nuovo stato \(\style{font-size:1em;}{\displaystyle \hat{O} | \psi \rangle}\). Quando si effettua una misurazione, il sistema “collassa” in uno degli autostati di quell’operatore, come indicato nell’equazione agli autovalori:

\( \style{font-size:1em;}{\displaystyle \hat{O} | \psi \rangle = o | \psi \rangle} \)

dove \(\style{font-size:1em;}{\displaystyle o}\) rappresenta l’autovalore, cioè il valore misurato dell’osservabile. Ad esempio, misurando l’energia di un elettrone in un atomo, si ottiene uno dei valori energetici \(\style{font-size:1em;}{\displaystyle E_n}\), e l’elettrone assume lo stato \(\style{font-size:1em;}{\displaystyle | E_n \rangle}\).

Un concetto fondamentale del formalismo di Dirac è il commutatore di due operatori \(\style{font-size:1em;}{\displaystyle \hat{A}}\) e \(\style{font-size:1em;}{\displaystyle \hat{B}}\), definito come:

\( \style{font-size:1em;}{\displaystyle [ \hat{A}, \hat{B} ] = \hat{A} \hat{B} – \hat{B} \hat{A}} \)

Se il commutatore risulta zero, le osservabili corrispondenti possono essere misurate simultaneamente; altrimenti, come nel caso di posizione e quantità di moto, il principio di indeterminazione limita la precisione con cui tali grandezze possono essere conosciute in simultanea.

Questo formalismo trova applicazione anche in contesti più complessi, come l’oscillatore armonico quantistico. Gli stati energetici dell’oscillatore sono quantizzati e indicati dai ket \(\style{font-size:1em;}{\displaystyle | n \rangle}\), dove \(\style{font-size:1em;}{\displaystyle n}\) identifica il livello energetico, e l’operatore hamiltoniano \(\style{font-size:1em;}{\displaystyle \hat{H}}\) agisce su di essi:

\(\style{font-size:1em;}{\displaystyle \hat{H} | n \rangle = E_n | n \rangle}\)

Gli operatori di creazione e distruzione, che modificano il numero quantico degli stati, vengono espressi nel formalismo di Dirac come:

\(\style{font-size:1em;}{\displaystyle \hat{a}^\dagger | n \rangle = \sqrt{n+1} | n+1 \rangle, \quad \hat{a} | n \rangle = \sqrt{n} | n-1 \rangle}\)

Infine, il formalismo di Dirac facilita il trattamento di sistemi entangled, dove due particelle sono correlate in modo tale che la misurazione di una influenzi l’altra. Lo stato entangled di due particelle si esprime come:

\( \style{font-size:1em;}{\displaystyle | \Psi \rangle = \frac{1}{\sqrt{2}} \left( | \uparrow \rangle_A | \downarrow \rangle_B – | \downarrow \rangle_A | \uparrow \rangle_B \right)} \)

Attraverso il formalismo di Dirac si semplificano i calcoli e si approfondisce la comprensione della natura probabilistica e non intuitiva del mondo quantistico.

Applicazioni del formalismo

Il formalismo di Dirac non è solo uno strumento matematico elegante per descrivere gli stati quantistici, ma costituisce anche una base solida per risolvere una vasta gamma di problemi in meccanica quantistica. Attraverso esempi concreti, si evidenzia come questo approccio sia indispensabile per comprendere fenomeni complessi e per sviluppare tecnologie avanzate.

Calcolo delle Probabilità di Transizione

Una delle prime applicazioni del formalismo è il calcolo delle probabilità di transizione tra stati quantistici. Se un sistema evolve da uno stato iniziale \(\style{font-size:1em;}{\displaystyle | \psi_i \rangle}\) a uno stato finale \(\style{font-size:1em;}{\displaystyle | \psi_f \rangle}\), la probabilità di questa transizione si esprime come:

\( \style{font-size:1em;}{\displaystyle P_{i \rightarrow f} = \left| \langle \psi_f | \psi_i \rangle \right|^2} \)

Questo calcolo risulta fondamentale in fenomeni quali l’assorbimento di fotoni da parte degli elettroni negli atomi, alla base della spettroscopia e della teoria delle perturbazioni.

Operatori di Creazione e Distruzione

Nella seconda quantizzazione, gli operatori di creazione e distruzione sono essenziali per descrivere sistemi con un numero variabile di particelle, come nei campi quantistici. Tali operatori modellano processi quali l’emissione di fotoni nei laser:

\(\style{font-size:1em;}{\displaystyle \hat{H} = \hbar \omega \left( \hat{a}^\dagger \hat{a} + \frac{1}{2} \right)}\)

Questo formalismo risulta imprescindibile nell’elettrodinamica quantistica, la teoria che tratta l’interazione tra luce e materia.

Stati Coerenti e Oscillatore Armonico Quantistico

Gli stati coerenti, che minimizzano l’incertezza tra posizione e quantità di moto, trovano largo impiego nell’ottica quantistica e nei laser. Nel formalismo di Dirac, tali stati sono autostati dell’operatore di distruzione:

\(\style{font-size:1em;}{\displaystyle \hat{a} | \alpha \rangle = \alpha | \alpha \rangle}\)

Questi stati, che richiamano le onde classiche, costituiscono un ponte tra la meccanica classica e quella quantistica.

Teoria delle Bande nei Solidi

Il formalismo di Dirac si rivela fondamentale per descrivere gli elettroni nei solidi, contribuendo alla comprensione delle bande di energia e dei semiconduttori, pilastri dell’elettronica moderna. La funzione d’onda di un elettrone in un cristallo si esprime come:

\( \style{font-size:1em;}{\displaystyle | \psi_{\vec{k}} \rangle = e^{i \vec{k} \cdot \vec{r}} | u_{\vec{k}} (\vec{r}) \rangle} \)

Questo approccio ha facilitato lo sviluppo di transistor, diodi e celle solari.

Spin e Magnetismo Quantistico

Il formalismo di Dirac permette di descrivere gli stati di spin delle particelle, concetto chiave nello studio del magnetismo e in tecnologie come la risonanza magnetica nucleare. Gli stati di spin sono indicati da ket come \(\style{font-size:1em;}{\displaystyle | \uparrow \rangle}\) e \(\style{font-size:1em;}{\displaystyle | \downarrow \rangle}\), mentre specifici operatori di spin agiscono su questi stati per delineare il comportamento magnetico.

Entanglement e Informazione Quantistica

Il formalismo di Dirac è essenziale per descrivere lo entanglement, risorsa fondamentale per la computazione quantistica e la crittografia quantistica. Uno stato entangled di due qubit si esprime come:

\(\style{font-size:1em;}{\displaystyle | \Phi^+ \rangle = \frac{1}{\sqrt{2}} \left( | 00 \rangle + | 11 \rangle \right)}\)

Questo formalismo è alla base di protocolli come la teleportazione quantistica e di algoritmi di computazione quantistica avanzati.

Scattering e Matrice S

Nello scattering quantistico, la matrice S descrive come uno stato iniziale \(\style{font-size:1em;}{\displaystyle | \psi_i \rangle}\) si evolve in uno stato finale \(\style{font-size:1em;}{\displaystyle | \psi_f \rangle}\) a seguito di un’interazione:

\( \style{font-size:1em;}{\displaystyle | \psi_f \rangle = \hat{S} | \psi_i \rangle} \)

Questa formalizzazione risulta cruciale nella fisica delle particelle, impiegata per analizzare le collisioni tra particelle ad alte energie, come negli esperimenti al Large Hadron Collider.

Stati Simmetrici e Antisimmetrici

Gli stati di bosoni e fermioni vengono descritti nel formalismo di Dirac tramite funzioni d’onda simmetriche o antisimmetriche. Ad esempio, per due fermioni si ha:

\( \style{font-size:1em;}{\displaystyle | \Psi_{\text{fermioni}} \rangle = \frac{1}{\sqrt{2}} \left( | \psi_a \rangle | \psi_b \rangle – | \psi_b \rangle | \psi_a \rangle \right)} \)

Questo approccio risulta essenziale per comprendere la struttura degli atomi e delle molecole, nonché per illustrare il principio di esclusione di Pauli.

Glossario dei termini chiave

Bra-Ket (Formalismo di Dirac): Una notazione matematica sviluppata da Paul Dirac in meccanica quantistica per rappresentare stati quantistici e operatori. Un ket \(\style{font-size:1em;}{\displaystyle | \psi \rangle}\) descrive uno stato quantistico, mentre un bra \(\style{font-size:1em;}{\displaystyle \langle \phi |}\) è il corrispondente operatore duale. Il prodotto \(\style{font-size:1em;}{\displaystyle \langle \phi | \psi \rangle}\) rappresenta l’ampiezza di probabilità di transizione tra stati.

Collasso della Funzione d’Onda: Processo in cui una funzione d’onda quantistica, che descrive una sovrapposizione di stati possibili, si riduce a uno stato definito a seguito di una misurazione.

Decoerenza Quantistica: Fenomeno per cui un sistema quantistico perde la coerenza (sovrapposizione di stati) a causa dell’interazione con l’ambiente esterno, portando a comportamenti classici.

Dualismo Onda-Particella: Principio della meccanica quantistica secondo cui le particelle elementari esibiscono sia proprietà ondulatorie che corpuscolari, a seconda delle condizioni sperimentali.

Entanglement (Intreccio Quantistico): Condizione in cui due o più particelle quantistiche sono correlate, così che lo stato di una dipende dallo stato dell’altra, indipendentemente dalla distanza che le separa.

Funzione d’Onda: Funzione matematica che descrive lo stato quantistico di un sistema e le probabilità associate ai possibili esiti delle misurazioni.

Interpretazione di Copenaghen: Interpretazione tradizionale della meccanica quantistica, secondo cui le proprietà fisiche non hanno valori definiti fino al momento della misurazione.

Operatore Hamiltoniano: Operatore che rappresenta l’energia totale di un sistema quantistico e descrive l’evoluzione temporale dello stato del sistema attraverso l’equazione di Schrödinger.

Oscillatore Armonico Quantistico: Modello base in meccanica quantistica che descrive un sistema che oscilla attorno a una posizione di equilibrio, con livelli energetici discreti.

Paradosso del Gatto di Schrödinger: Esperimento mentale ideato da Erwin Schrödinger per mostrare le implicazioni paradossali della sovrapposizione quantistica in sistemi macroscopici.

Principio di Indeterminazione di Heisenberg: Principio fondamentale secondo cui non è possibile conoscere simultaneamente e con precisione coppie di proprietà come posizione e quantità di moto.

Principio di Sovrapposizione: Principio per cui un sistema quantistico può esistere in una combinazione lineare di più stati fino alla misurazione.

Quantizzazione dell’Energia: Fenomeno per cui l’energia di un sistema quantistico assume valori discreti piuttosto che continui, come accade nella fisica classica.

Qubit (Quantum Bit): Unità di informazione quantistica che può esistere in sovrapposizione di stati “0” e “1”, a differenza dei bit classici.

Spin: Proprietà intrinseca delle particelle quantistiche, interpretabile come una forma di momento angolare intrinseco, senza un’analogia diretta nel mondo classico.

Teoria dei Campi Quantistici: Quadro teorico che combina meccanica quantistica e relatività speciale per descrivere i campi quantizzati e le interazioni tra particelle.

Transizione Quantistica: Passaggio di un sistema quantistico tra stati energetici, spesso associato all’emissione o assorbimento di un fotone.

Variabili Nascoste: Ipotesi secondo cui l’indeterminazione in meccanica quantistica deriva da fattori non osservabili. Teorie di variabili nascoste locali sono state confutate dagli esperimenti.